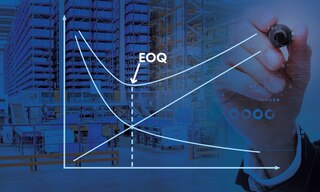
Ekonomiczna wielkość partii (EOQ) – sposób obliczenia i zastosowanie

Sklepy detaliczne oraz internetowe muszą skrupulatnie monitorować swój asortyment. Nadmierny poziom zapasów może wiązać się z wyższymi kosztami, z kolei zbyt niski – prowadzić do utraty możliwości sprzedaży. Model EOQ (ang. Economic Order Quantity) jest jednym z narzędzi dostępnych dla każdej firmy, umożliwiającym osiągnięcie optymalnego stanu zapasów.

EOQ – co to jest i do czego służy?

EOQ, czyli ekonomiczna wielkość partii, to metoda zarządzania asortymentem określająca optymalną liczbę produktów do zakupienia, aby zminimalizować koszty związane z transakcją, składowaniem towaru oraz uzupełnianiem zapasów. Ma na celu usystematyzowanie zapasów w magazynie i określenie dat składania zamówień u dostawców oraz ich proporcji.

Zalety i wady EOQ

Obliczanie EOQ ma kilka zalet, m.in. zrównoważenie poziomu asortymentu, zmniejszenie ryzyka powstawania odpadów i starzenia się produktów czy optymalizacja przepływu pojemników oraz inwestowanie kapitału obrotowego. Wszystko to odbywa się z uwzględnieniem popytu i minimalnego poziomu zapasu zabezpieczającego. Oszacowanie poziomu sprzedaży produktu umożliwia wyznaczenie terminu złożenia zamówienia oraz określenie liczby produktów, którą należy nabyć, aby osiągnąć optymalny stan zapasów.

Model ekonomicznej wielkości partii działa przy założeniu, że popyt, czas dostawy, cena zamówienia i koszty utrzymania są stałe. Technika ta jest powszechnie stosowana w przypadku operacji logistycznych ze względu na jej prostotę oraz ogólnie trafne prognozy i szacunki, ale nie obejmuje kampanii jednorazowych oraz sezonowych, opóźnień w uzupełnianiu zapasów ani rabatów ilościowych.

Jak obliczyć model EOQ?

Podczas ustalania optymalnej wartości EOQ należy wziąć pod uwagę następujące czynniki:

• Koszt zamówienia. Każde zlecenie zakupu, jego przetwarzanie i dostarczenie wiąże się z wydatkiem.
• Koszty utrzymania asortymentu. Składowanie artykułów przez określony czas sprawia, że cena jednostkowa przedmiotu obejmuje ubezpieczenie i uszkodzenia. Jest to wyrażone jako koszt jednostkowy na dany okres.
• Całkowity koszt. Suma dwóch powyższych. Poznanie tej wartości ma na celu umożliwienie jej zmniejszenia.

Wzór na obliczenie ekonomicznej wielkości partii (EOQ)

Na podstawie wcześniej omówionych zmiennych ekonomiczna wielkość partii (EOQ) jest reprezentowana jako roczne zapotrzebowanie na dany produkt (D), koszt złożenia zamówienia (K) oraz działań związanych ze składowaniem jednostki w magazynie przez cały rok (G).

​

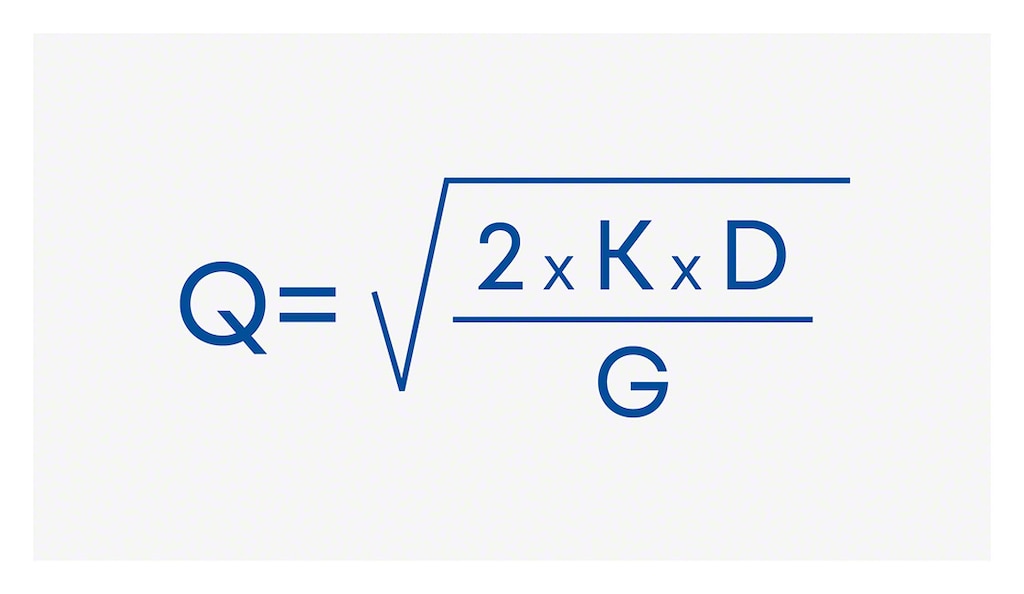
Należy pamiętać, że obliczenia te nie uwzględniają przestrzeni, jaką się dysponuje do składowania rekomendowanej liczby produktów. Jeśli wartości się nie pokrywają, możliwe jest ponowne obliczenie EOQ lub znalezienie alternatywnego wykorzystania przestrzeni przy pomocy doradztwa logistycznego.

Przykładowe zastosowanie modelu EOQ

Firma A dystrybuuje duże płytki, a jej roczny popyt wynosi 4000 sztuk (D). Koszt każdego zamówienia lub zakupu materiału i powiązanych z nim kosztów (K) wzrasta do 100 €, a składowanie każdej płytki w ciągu roku kosztuje 4 € (G).

Po zastosowaniu tego wzoru otrzymujemy wartość EOQ wynoszącą 447 płytek. Dlatego firma powinna każdorazowo zamawiać taką liczbę sztuk.

Wynika więc, że dana firma powinna składać co najmniej dziewięć zamówień w ciagu roku, składających się z 447 sztuk, aby w sumie nabyć około 4000 płytek.

Kto stworzył model EOQ?

Za twórcę EOQ uważany jest pochodzący ze Stanów Zjednoczonych inżynier produkcji Ford Whitman Harris. Pracownik Westinghouse Electric and Manufacturing Company opublikował artykuł How many parts to make at once na łamach magazynu „Factory, The Magazine of Management” w 1913 roku. Jednakże ekonomiczna wielkość partii rozpowszechniła się dopiero w 1934 za sprawą R. H. Wilsona, który dopracował model znany obecnie jako formuła Wilsona.

Formuła EOQ w praktyce

Zastosowanie formuły EOQ zapewnia kluczowe dane do zarządzania zapasami, warto jednak podjąć dalsze działania, aby sprawdzić, czy aktualne ilości mogłyby być nieco bardziej ekonomiczne:

1. Identyfikacja głównych kosztów w łańcuchu dostaw.
2. Określenie konkretnych dochodów związanych z każdą grupą obsługiwanych artykułów.
3. Obliczenie modelu EOQ dla każdego produktu.
4. Porównanie wyników zastosowanej formuły z bieżącymi zamówieniami.
5. Podjęcie działań i wdrożenie zmian w zarządzaniu z dostawcami.
6. Częste przeliczanie EOQ, szczególnie w przypadku zmian w zakresie kosztów zamówień i popytu na produkty.

W ten sposób można ocenić opłacalność zamówień składanych u dostawców. Dysponowanie kompleksowymi danymi o działaniach logistycznych firmy, obejmującymi więcej informacji niż roczna sprzedaż, koszty przesyłek i działań mającymi na celu utrzymanie jednostek ładunkowych w magazynie przez cały rok, jest wielką pomocą w poprawie wydajności centr logistycznych.

Jeśli chcesz uzyskać pełny wgląd w procesy przeprowadzane w Twojej firmie, skontaktuj się z nami. Mecalux od 1966 roku specjalizuje się w logistyce magazynowej. Nasi eksperci opracowali system zarządzania magazynem służący do osiągnięcia maksymalnej wydajności łańcucha dostaw. Pomożemy Ci wybrać system, który najlepiej dostosuje się do Twoich potrzeb, a jeśli w Twoim magazynie brakuje miejsca na składowanie EOQ, przeanalizujemy możliwości zoptymalizowania Twojej instalacji za pomocą rozwiązań magazynowych.